이 리뷰는 오직 학습과 참고 목적으로 작성되었으며, 해당 논문을 통해 얻은 통찰력과 지식을 공유하고자 하는 의도에서 작성된 것입니다. 본 리뷰를 통해 수익을 창출하는 것이 아니라, 제 학습과 연구를 위한 공부의 일환으로 작성되었음을 미리 알려드립니다.
이 논문은 Continuous Normalizing Flows(CNF)를 시뮬레이션 없이 효율적으로 학습할 수 있는 방법으로 Flow Matching(FM)을 제안한다. 최근 생성 모델에서 Flow Matching 관심을 끌고 있는 만큼, 논문을 리뷰해 보게 되었다.
https://arxiv.org/abs/2210.02747
Flow Matching for Generative Modeling
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs base
arxiv.org
1. Introduction
최근 몇 년간 생성 모델 분야에서 디퓨전(diffusion) 계열 모델은 탁월한 성능을 보여주며 사실상 주류로 자리 잡았다. 여러 단계에 걸친 반복적 샘플링을 통해 고품질의 이미지를 생성할 수 있다는 점은 큰 장점이지만, 동시에 이러한 과정은 추론 속도를 심각하게 저하시킨다는 한계를 지닌다.
본 논문은 Continuous Normalizing Flows(CNF)를 시뮬레이션 없이(simulation-free) 효율적으로 학습할 수 있는 새로운 훈련 방법으로서 Flow Matching(FM)을 제안한다. 이 글에서는 해당 논문을 중심으로 Flow Matching의 핵심 아이디어와 기여점을 정리하고자 한다.
Simulation-Free? CNF? 하나씩 알아보자
2. Continuous Normalizing Flows
Recap) 우선 이전 생성모델의 구조를 살펴보자

생성모델 : 데이터의 분포를 학습 ( Source(p0) 분포에서 Target(p1) 분포로 변화되는 과정을 학습 )
- GAN, VAE
- 대부분의 생성 모델은 샘플링이 쉬운 분포(예: 가우시안 분포) z에서 데이터 분포 x로의 변환을 학습한다.
- GAN: z → x 변환을 적대적 학습(Adversarial Training)을 통해 학습한다.
- VAE: z → x 생성과 x → z 인코딩을 동시에 학습해 잠재공간을 정규화한다.

=> GAN, VAE 같은 모델은 Source(p0) 분포에서 Target(p1) 분포를 한번에 mapping하는 방식
- Diffusion model

- Diffusion model: x → z 방향으로 점진적으로 노이즈를 주입하는 과정을 학습하고, 반대로 z → x 방향으로 노이즈 제거(Denoising) 과정을 통해 데이터를 생성한다. => 노이즈 제거 함수를 학습
- 복잡한 데이터 분포 학습 가능, 학습이 효율적 But 생성속도가 느림
- 하지만 생성속도가 느림 ( 여러번의 model forward )
=> Diffusion model Source(p0)분포에서Target(p1)분포로 단계적으로 변화
- Normalizing flow ( Flow 모델 , NICE )
- Normalizing flow : x → z로의 가역적 변환(flow)을 학습하고, 역변환을 통해 z → x 생성을 수행한다.
- Likelihood를 계산 가능하다는 장점이 있음 => 확률추정이 가능
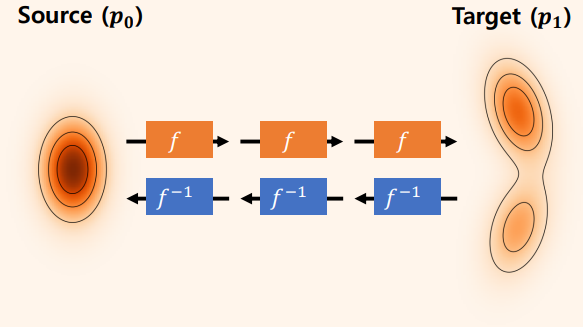
Normalizing flow 모델은 역변환이 가능한 모델 구조(Jacobian determinant 계산 가능)가 필요하고, 학습이 비효율적이다 ( 역변환을 계속 해야하기 때문에 ).
https://angeloyeo.github.io/2020/07/24/Jacobian.html
자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
Flow model?
Source(p0)를 Target(p1)로 변환하는 Flow를 찾는 모델
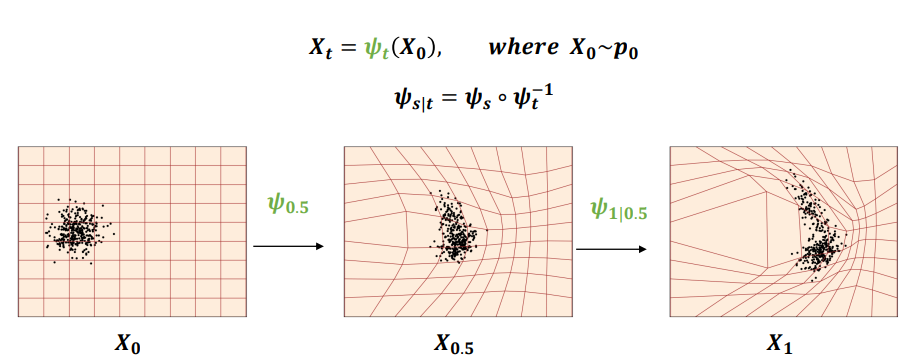
- Flow model: source 분포 𝑝0를 target 분포 𝑝1으로 변환해주는 flow(𝝍𝒕)를 찾는 모델 싸이t
- Flow? 𝑋0를 𝑋𝑡 로 Mapping해주는 함수 (Diffeomorphism <= 특징 [미분가능 / 역함수 존재])
- 하지만 Continuous time(중간중간 샘플이 없는) 상황에서 flow를 직접적으로 학습하기는 어려움
이해를 돕자면 Flow는 데이터 분포와 간단한 분포(보통 정규분포)를 연결하는 변환이며

자체를 학습해서 데이터 분포를 얻음, 즉 Flow 자체를 파라미터화해서 학습
그래서 Flow model에서는 vector field를 통해 flow를 간접적으로 계산
- Velocity Field (vector field)
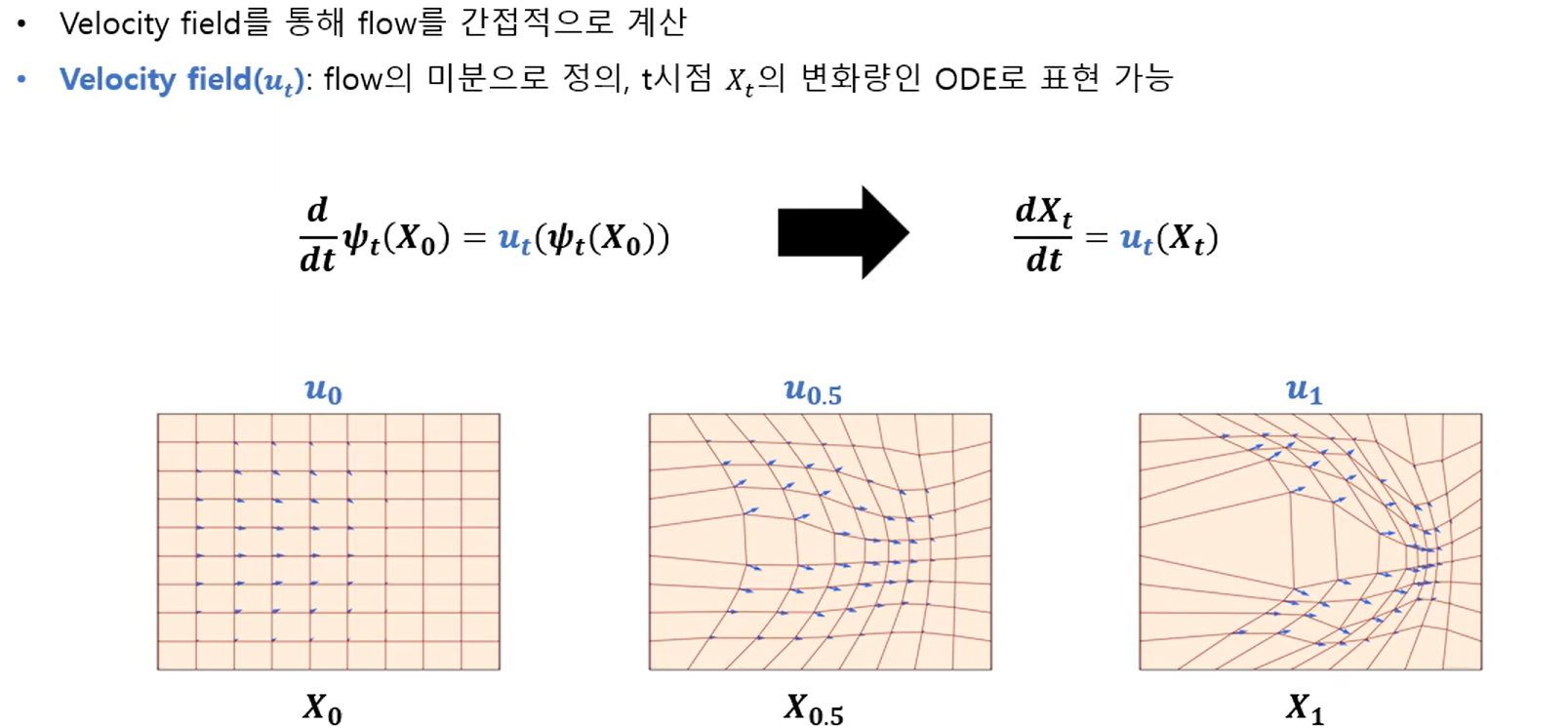
Flow를 간접적으로 계산하는 과정, 간단하게 𝝍𝒕(X) = Flow를 t에 대해 미분하는 것
- 한마디로 Velocity Field는 각각의 포인트에서 화살표 방향이다. 어디로 갈지, 즉 각각의 점에서 어디로 움직여야 소스에서 타겟으로 옮겨갈 수 있나를 알려주는것을 Velocity Field라고 한다. ODE로 정의됨
Flow의 미분을 통해 Velocity filed를 구하고 Solver를 통해 다시 Flow를 구할 수 있음

스탭h를 지정한뒤 Velocity Field와 Solver 를 통해 t일 떄 타겟분포 Xt를 구할 수 있다.
+ Probability Paths

Probability Paths(pt) = 그렇게 source 분포 𝑝0에서 target 분포 𝑝1로 가는 과정의 t시점의 분포를 말함
- Normalizing Flow(NF):
- x → z (데이터 분포 → 잠재 분포)로 가는 가역적인 변환 f를 뉴럴 네트워크가 학습한다.
- 학습 후에는 z0 ~ N(0, I)를 샘플링한 뒤 f⁻¹(z0)을 통해 데이터를 생성할 수 있다.
- 쉽게 말하자면 데이터 분포인 에서 로의 역변환이 가능한 함수(Flow)를 학습하는 모델
- Continuous Normalizing Flow(CNF):
- 변환 함수 자체를 학습하는 대신, vector field를 학습한다.
- 시간축 t ∈ [0, 1]을 따라 정의된 흐름(flow)에서,
- t=0일 때 분포는 z,
- t=1일 때 분포는 x가 된다.
- 따라서, z에서 출발해 ODE Solver로 적분하면 최종적으로 데이터 분포 샘플을 생성할 수 있다.
- 장점: 역변환 가능해야 한다는 제약 해소.
- 단점: 학습과 샘플링 과정에서 ODE Solver(수치적분)을 반복적으로 호출해야 하므로 비용이 크다. → Diffusion의 느린 샘플링 문제와 유사, "ODE의 적분에는 많은 시간이 걸린다
NF가 복잡한 분포에 맞게 함수 파라미터 최적화 한다면 CNF는 시간에 따라 분포가 맞게 흘러가도록 vector field 최적화
정리:
Data: d차원 벡터 공간에 존재하는 포인트
Flow(ϕ): 데이터를 시간에 따라 연속적으로 변환하는 함수. ODE(미분 방정식)
Vector Field: 데이터 공간의 각 위치에서 어떤 방향으로 얼마나 이동할지를 나타내는 정보
Probability density path(p): 시간에 따라 변화하는 확률 밀도 함수
Continuous Normalizing Flow(CNF): 위의 vector field를 neural network로 나타낸 모델, 연속적인 시간 변화에 따른 데이터 변환을 모델링. 즉, 간단한 데이터 분포에서 복잡한 분포로 변환하는 역할
Flow Matching (FM)
Flow mathcing은 적분 없이 Velocity Field를 학습, 즉 Flow Matching은 CNF를 학습하기 위한 새로운 목적 함수로 vector field를 학습하도록 하는 것
CNF는 굉장히 강력한 프레임워크이지만 많은 데이터셋에 대해서 학습하기가 굉장히 어렵다. 학습 과정 중에 적분을 수행해야 하기 때문에 ODE Solver를 통해서 여러번의 forward가 필요하기 때문이다. 간단하게 말해서, Diffusion 모델의 느린 샘플링 과정을 매 학습마다 수행해야 하는 것이다. 목표인 Flow Matching이 어떻게 simulation-free, 즉 실제 적분 과정 없이 CNF를 학습 가능하게 하는지를 알아보자.

CNF처럼 vector field를 학습하지만 직접 밀도를 계산하지 않고 학습해야한다. x1는 우리가 알지 못하는 q(x1)데이터의 분포 에서 얻은 샘플들로, 생성 모델을 훈련하고자 하는 데이터셋이다. pt를 정의할 것인데, 는 우리가 알고 있는 쉬운 분포p가 p0이고, p1 되도록 하고 싶다.

데이터 샘플을 갖고 있지만, 데이터 분포 함수 자체는 알지 못한 상태에서 목표 u와 v가 같아지도록 regression, 손실 함수가 0에 가까워지면 CNF 모델이 probability path p를 생성할 수 있다. 하지만 우리는 p와 u를 모르기 때문에 Flow Matching은 probability path에 대한 supervision을 사용하여 로스를 사용할 수 있게 한다. 우리가 직접 p와 u를 만들어주는 것이다. 당연히 전체 분포에 대한 것을 임의로 만들 수는 없고 샘플 별로 p와 u를 디자인해주는데 어떻게 하는지 살펴보자.
Conditional Flow Matching (CFM)
1. pt와 ut를 정의
- Conditional probability path(조건부 확률 경로, )
- t=0일 때 는 간단한 초기 분포 p(x).
- t=1일 때 는 평균이 이고, 작은 표준편차를 가지는 정규분포
- Marginal probability path(주변 확률 경로, ): 여러 조건부 확률 경로를 합친 결과

Marginal Vector field(주변 벡터 필드, )
- 조건부 벡터 필드()는 각 조건부 확률 경로 를 생성하는 벡터 필드

조건부 벡터 필드들을 모두 합친 것이 주변 벡터 필드
위의 수식에서 은 특정 샘플 에 대해서 간단한 분포의 x가 어떻게 이동해야 하는지 나타내고 는 가중치로, 각 데이터 샘플에 대한 conditional vector field()가 marginal vector field()에 얼마나 기여하는지를 결정한다.
Theorem1: 조건부 문제들을 잘 정의하고 이를 마진화하여 합치면 전체적인 분포를 생성할 수 있는 유효한 벡터 필드를 얻을 수 있다는 것을 보장합니다.
2. Conditional flow matching

이전 단락에서 설명한 marginal probability path와 vector field는 적분 계산이 복잡하고 직접 계산하기 어려운 난해한 수식을 포함함. 따라서 Flow mathcing 목표를 계산하는 것은 비현실적이다. 이에 따라 Conditional flow matching loss이라는 더 간단한 목표를 제안한다.
- t∼U[0,1]은 균등 분포를 따르는 시간
- 은 데이터 분포에서 샘플링한 데이터.
- 은 조건부 확률 경로에서 샘플링한 데이터
Theorem2:

그리고 여기서 두 로스가 같다는 증명이 등장한다. 즉, sample 별로 최적화를 수행하고 expectation을 구하는 식으로 최적화를 진행해도 된다는 뜻이다. 증명은 논문의 Appendix에 있다. 이걸로 적당한 supervision을 통해 ode solver 필요 없이 CNF를 학습하는 방법을 알았다. 이제 필요한 것은 적절한 p, u를 정의하는 것이다.
probability path 를 실제로 정의하여 conditional path (우리의 “label” 이 될 대상) 을 구체화시켜보자.
(1) Probability path p 정의
논문에서는 probability path로 gaussian distribution을 사용한다.

x1에대한 평균과 표준편차를 사용하여 정규분포로 가정, 와 에 대한 조건을 아래와 같이 사용한다.
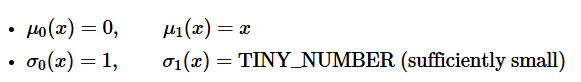
t=0일 때 평균은 0, 표준편차를 1, t=1일 때 평균을 x, 표준편차를 충분히 작은값으로 설정하였을 때 다음과 같은 Flow를 얻을 수 있다.


그리고 앞에서와 같은 flow를 시점 t에 대하여 미분하여 vector 필드를 구할 수 있다.

Theorem3: 최종적으로 백터필드는 위와같은 수식으로 구할 수 있다.
정리하자면 Continuous Normalizing Flows(CNF)는 데이터 분포를 학습하기 위해 ODE 적분을 사용하였음. 그러나 이러한 적분 과정은 계산량이 많고 시간이 오래 걸리는 문제가 있었다. 이를 개선하기 위해 augmentation이나 regularization을 추가하는 방식의 연구들이 진행되었으나, 이는 ODE를 정규화한 것에 불과하고 학습 알고리즘 자체를 변화시키지는 못했다.
CNF 학습 속도를 높이기 위해 simulation-free CNF training frameworks가 개발되었다. 하지만 이러한 방식 역시 여전히 적분 계산의 부담이 있었고, Flow Matching은 이러한 한계를 극복하기 위해 제안된 방법으로, 시뮬레이션 과정조차 필요 없이 CNF를 학습할 수 있도록 하였다. 이로써 단순하고 빠른 학습이 가능해졌다
Flow Matching의 Conditional Flow Matching(CFM)은 diffusion 기반 설계에서 출발하였으나, 벡터 필드를 직접 매칭하는 접근 방식을 일반화하였음. 따라서 Flow Matching은 처음으로 diffusion 과정 없이 확률 경로를 직접 학습할 수 있음을 보여주었으며, CNF 학습의 새로운 가능성을 제시하였다.
- 참고자료
https://arxiv.org/abs/2210.02747
Flow Matching for Generative Modeling
We introduce a new paradigm for generative modeling built on Continuous Normalizing Flows (CNFs), allowing us to train CNFs at unprecedented scale. Specifically, we present the notion of Flow Matching (FM), a simulation-free approach for training CNFs base
arxiv.org
https://youtu.be/YFZbFr3cjpA?si=K4yX3xw-CTp1Y3wv
https://seastar105.tistory.com/176
Flow Matching 설명
Introduction 디퓨전 계열이 생성 모델에서 엄청난 성능을 보여주며 주류가 되어 버린지는 한참 되었다. 그러나 여러 번에 걸친 샘플링이 디퓨전 모델의 좋은 성능을 만들어 주는 것처럼 보이지만
seastar105.tistory.com
'Computer Vision > Paper reviews' 카테고리의 다른 글
| [Object Detection] One-Stage Object Detection - YOLO, SSD, RetinaNet (0) | 2025.09.12 |
|---|---|
| [ILSVRC 논문 정리해 보기] DenseNet, SENet과 대회 그 이후 (0) | 2025.09.05 |
| [ILSVRC 논문 정리해 보기] VGGNet, GoogleNet, ResNet (0) | 2025.09.05 |
| [Object Detection] Faster R-CNN (0) | 2025.08.06 |
| [Object Detection] SPPNet과 Fast R-CNN (0) | 2025.07.17 |
