- 에지 검촐과 영역 분할의 차이
- 에지는 특성이 다른 곳을 검출하지만 영역은 유사한 화소를 묶는 방법을 사용한다
- 사람은 의미 분할에 능숙, 사람은 머리속에 기억된 물체 모델을 이용하여 의미 분할
- 딥러닝을 이용해야 의미 분할이 가능함 ( semantic segmentaion )
에지 검출
- 물체 내부나 배경은 변화가 작거나 없는 반면 물체 경계는 변화가 큼
- 이 원리에 따라 에지 검출 알고리즘은 명암, 컬러, 또는 변화량을 측정하고, 변화량이 큰 곳을 에지로 검출한다.
영상은 이산 공간, △x는 극한으로 가도 0이 아닌 1

- 이를 대입해보면

- 변화량을 절대값과 임계값을 설정
- 계단 에지와 램프 에지

- 계단 에지는 찾기 쉽지만 램프 에지는 찾기 힘들다
- 자연 영상에서는 주로 램프 에지가 나타남
- 1차 미분으로 램프 에지를 찾기 어렵다
- 1차 미분을 2번 하여 검출, 2차 미분값에서 영 교차가 일어남
- +~-, -~+로 가는 0을 거쳐지나가 이것을 제로 크로싱, 영교차라고 한다
- 라플리시안

- 미분 2번하면 1 -2 1 마스크 쓰는거랑 똑같음

- 0교차가 일어나는 부분을 엣지로 결정

- 현실에서는 잡음을 스무딩필요
- 엣지를 찾기 전에 스무딩을 실시

- 모든 편미분을 모아둔 것을 그레디언트 벡터라고 함
- y방향의 편미분, x방향의 편미분, 즉 기울기를 모아둔것

- 주변 영역을 확장해서 계산
- 해당 픽셀 방량에 가중을 준 것이 소벨 연산자
- 로버츠는 대각선 방향

- 각각 변화량의 크기를 에지 강도 S 라고 함
- 변화량의 각도를 D 그레디언트 방향이라고 함
- 세타

- 세타
- 그레디언트 방향과 수직인 백터를 에지 방향이라고 함
- 에지 방향을 보고 섰을 때 왼쪽은 밝고 오른쪽은 어두운 방향으로 결정
- 일관성만 유지하면 됨

- 이 이미지에서 밝은쪽을 오른쪽이라고 하면 에지 방향이 반대가 됨

- 다음 그림으로 양자화 해놓음
- 위 이미지를 예시로 하면 에지 방향은 5

- dx = -4, dy = 2
- S(5,3) = 루트20
- D(5,3) = 그레디언트 방량 = arctan(-4/2) = -63.4

- 영상 이미지에서는 오른쪽이 + 방향 ( 시계방향 )
- 에지 방향은
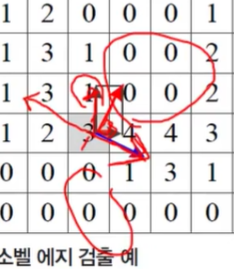
- dx>0, dy<0 이라면 에지 방향은 -90 ~ 90
- 최종 에지 방향은 90 - 63.4 = 26.6 이다.
캐니 에지
- 에지 검출을 최적화 문제로 해결, 현재 가장 널리 사용
- 최소 오류율 : 거짓 긍정과 거짓 부정이 최소여야 한다. 즉 없는 에지가 생성되거나 있는 에지를 못 찾는 경우를 최소로 유지해야 한다.
- 위치 정확도 : 검출된 에지는 실제 에지의 위치와 가급적 가까워야 한다.
- 에지 두께 : 실제 에지에 해당하는 곳에는 한 두께의 에지만 생성해야한다

- 비최대 억제(에지에서 제거)
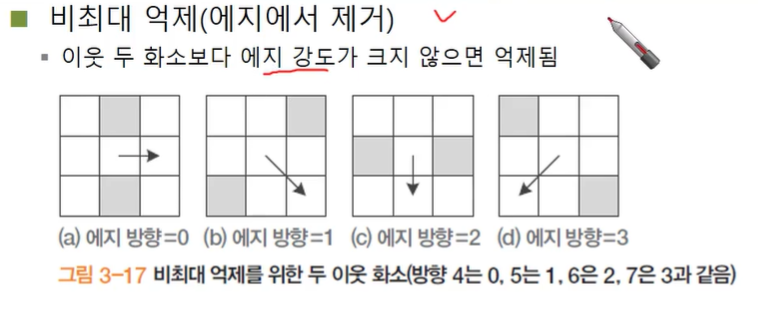
- 에지 방향을 찾아서 이웃 두 화소보다 에지 강도가 크지 않으면 억제
- 이력 임계값
- 두개의 임계값을 사용해서 거짓 긍정을 줄임

- maxVal로 에지를 찾은 다음 minVal보다 큰 값중 maxVal에 연결되 있지 않은 값은 제거
- 높은 임계값과 낮은 임계값의 비율을 2:1, 3:1로 하면 좋다

- 시그마가 커질 수록 디테일이 사라짐
- 임계값이 커질 수록 디테일이 사라짐
- 캐니 알고리즘을 통해
- 이웃 엣지 연결
- 경계선을 직선으로 근사 변환
- 에지를 명시적으로 연결하여 경계선을 찾고 직선으로 변환해야함
경계선 찾기

- 허프 변환
- 에지 연결 과정 없이 선분을 찾는 방법 ( 전역 연산을 이용한 지각 군집화 )

- x,y 공간을 a,b 공간으로 변경
- y1,x1 을 a,b 공간으로 맵핑한다고 한다면
- y = ax+b ⇒ b = -xa + y
- 기울기가 -x , 절편이 y인 직선이 되는데
- 이는 y1,x1 점을 지나가는 모든 직선이 됨
- 여기서 세 점을 지나는 직선의 기울기 a1과 b1은 a,b 공간상의 직선들의 교점의 좌표 (a1,b1)과 같다
- 수직이나 수평(기울기가 0 또는 1)의 직선이 있으면 찾을 수 없음
- 극좌표계를 사용하여 기울기가 무한대인 문제를 해결
- x,y 공간을 로,세타 공간으로 보냄 ( p, θ )
- ycosθ + xsinθ = p

- θ 값이 주어졌을 때 p 구하는 방법

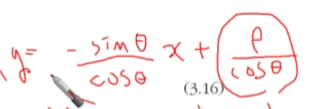
- 예제

- 지나치는 점을 중첩해서 찾아내면 3이되는 곳을 찾을 수 있다.
- 그 점을 다시 y,x의 좌표로 변환한다. // θ 와 p를 알기 때문에 굳이 바꾸지 않아도 괜찮을 듯..?
- 하지만 3이 매번 생기는 것이 아니기 때문에 적합한 모델을 찾아줘야 함
영상에서 허프 변환으로 선 검출 ( 극 좌표계 사용 )
- 직선의 방정식 y = ax + b 를 사용할 때의 문제점
- y 축과 평행한 수직선을 표현하지 못함(a: 무한대)
- 극좌표계 형태의 직선의 방정식을 사용


RANSAC

- 랜덤 샘플링: 주어진 데이터에서 임의의 샘플을 선택하여 모델을 생성.
- 모델 평가: 생성된 모델을 전체 데이터에 적용하여 내부 모델(잘 맞는 데이터)과 이상치(모델에 맞지 않는 데이터)를 구분.
- 반복: 이 과정을 여러 번 반복하여 가장 많은 내부 모델을 가진 모델을 선택.
- 모델 선택: 반복 후 가장 적합한 모델을 최종 모델로 결정.
'Computer Vision > Basic' 카테고리의 다른 글
| [CV 기초] #6 영역 특징 (4) | 2024.04.06 |
|---|---|
| [CV 기초] #5 영상 분할 (6) | 2024.04.06 |
| [CV 기초] #3 모폴로지와 컨볼루션 (4) | 2024.03.26 |
| [CV 기초] #2 인식 성능 측정 (1) | 2024.03.26 |
| [CV 기초] #1 컴퓨터 비전 (1) | 2024.03.26 |