[Project] 도시 데이터를 활용한 길거리 쓰레기통 배치 최적화 해보기

Part 3. 마포구 데이터를 이용하여 적절한 쓰레기통 갯수를 예측하고 배치 최적화 해보기

 

이전글

2025.06.02 - [Data Analysis/Project] - [Project] 데이터를 활용하여 가중치 그리드 만들기

[Project] 데이터를 활용하여 가중치 그리드 만들기

 

연도별 추세 분석을 통한 적절한 쓰레기통 개수 예측

1. 마포구 연도별 가로 쓰레기통 변화 분석

• 마포구의 가로 쓰레기통 설치 수는 주로 주민 민원이나 행정 정책 변화에 따라 증가하거나 감소해 왔음음
• 하지만 우리는는 쓰레기통의 연도별 데이터를 기반으로 추세를 분석하고 향후 예측값을 도출하는 방식으로 접근
• 이러한 예측값을 바탕으로, 쓰레기통이 실제로 필요한 곳에 효율적으로 배치되도록 최적화하는 데 중점을 두었음음

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

plt.rcParams['font.family'] = 'Malgun Gothic'
plt.rcParams['axes.unicode_minus'] = False

df = pd.read_excel("seoul_street_bin_count_by_year_2013_2024.xlsx")
mapo_row = df[df['자치구'].str.strip() == '마포구'].iloc[0, 1:]  # 마포구에서 연도 컬럼만 추출

# 열 이름에서 숫자만 추출
years = mapo_row.index.astype(str).str.extract(r'(\d{4})')[0].astype(int)

# 쉼표 및 공백 제거, 정수형으로
bin_counts = mapo_row.apply(lambda x: int(str(x).replace(',', '').strip()))

# 증가율 계산
growth_rate = bin_counts.pct_change().fillna(0) * 100

bin_df_clean = pd.DataFrame({
    "연도": years,
    "쓰레기통수": bin_counts.values
})

# 시각화
plt.figure(figsize=(10, 5))
plt.plot(years, bin_counts, marker='o', color='darkgreen', linewidth=2)
plt.title("마포구 연도별 가로 쓰레기통 수 변화")
plt.xlabel("연도")
plt.ylabel("쓰레기통 수")
plt.grid(True)
plt.xticks(years)
plt.tight_layout()
plt.show()

# 표 출력
summary_df = pd.DataFrame({
    '연도': years,
    '쓰레기통 수': bin_counts.values,
    '증가율(%)': growth_rate.values.round(2)
})

display(summary_df)

 

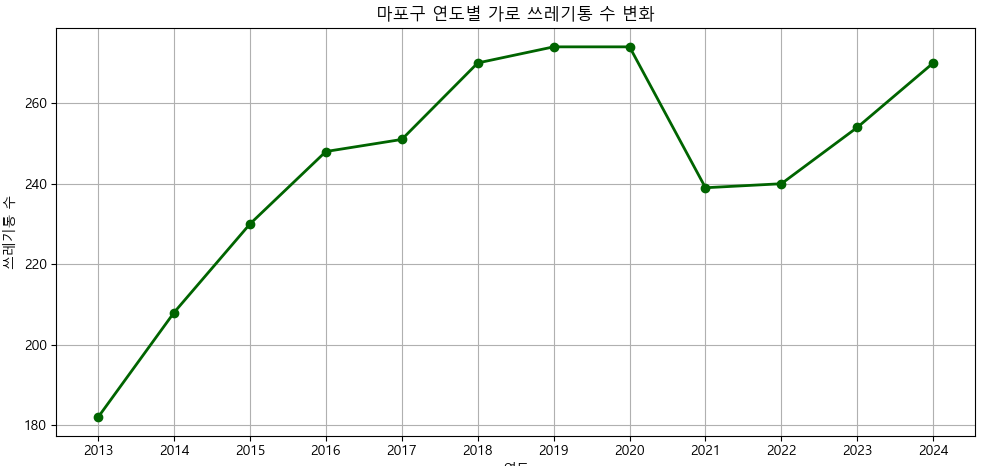
• 2013~2018년까지는 꾸준히 증가하는 추세를 보임.
• 2019~2020년에는 성장이 거의 정체됨.
• 2020년에는 무단투기 문제로 가로 쓰래기통을 일부 철거 쓰레기통 주변 무단투기 문제, 민원 등을 종합적으로 고려했다는 이유에서였다. 출처 : 더스쿠프(https://www.thescoop.co.kr/news/articleView.html?idxno=303162)]
• 이후 다시 점진적인 증가세로 전환되어 2024년에는 270개로 회복.

 

2. 연도별 매출 추이 분석

• 마포구 내 각 상권의 매출 금액과 해당 업종의 업종별 가중치(총점) 를 곱하여 ‘가중 매출’을 계산함
• 이를 연도별로 집계하여, 시간에 따른 가중 매출의 변화 추이를 선형 회귀를 통해 분석함
• 아래 그래프는 연도별 총 가중 매출과 회귀선을 시각화한 결과임

from sklearn.linear_model import LinearRegression

# 데이터 불러오기
sales_df = pd.read_csv("mapo_sales_trash_score_2020_2024.csv", encoding="cp949")
sales_df['총점'] = sales_df['총점'].fillna(0)
sales_df['가중_매출'] = sales_df['당월_매출_금액'] * sales_df['총점']

# 연도별 집계
weighted_sales = sales_df.groupby("연도")["가중_매출"].sum().reset_index()
weighted_sales.columns = ["연도", "총_가중_매출"]

# 선형 회귀 학습
X = weighted_sales[["연도"]]
y = weighted_sales["총_가중_매출"]
model = LinearRegression().fit(X, y)

# 2025년 예측
X_future = pd.DataFrame({'연도': [2025]})
y_future = model.predict(X_future)[0]

extended_sales = pd.concat([
    weighted_sales,
    pd.DataFrame({'연도': [2025], '총_가중_매출': [y_future]})
], ignore_index=True)

# 회귀선 범위 (2020~2025)
X_line = pd.DataFrame({'연도': list(weighted_sales["연도"]) + [2025]})
y_line = model.predict(X_line)

# 시각화
plt.figure(figsize=(9, 5))
plt.plot(weighted_sales["연도"], weighted_sales["총_가중_매출"], marker="o", color="green", label="총 가중 매출")
plt.plot(X_line["연도"], y_line, linestyle="--", color="blue", label="선형 회귀 추세선")
plt.title("연도별 총 가중 매출 추이 및 2025년 예측값 표시")
plt.xlabel("연도")
plt.ylabel("총 가중 매출 (원)")
plt.xticks(list(weighted_sales["연도"]) + [2025])
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

 

3. 연도별 생활인구 변화 분석

• 마포구의 시간대별 생활인구 데이터를 연도 단위로 집계하여 평균 생활인구와 최대 생활인구의 변화 추이를 분석함
• 각 항목별로 선형 회귀를 적용하여 2025년의 생활인구를 예측

# 데이터 불러오기
pop_df = pd.read_csv("mapo_population_by_hour_2020_2024.csv", encoding="cp949")

# 연도별 생활인구 합계 계산
yearly_pop = pop_df.groupby("연도")[["시간별평균생활인구수", "시간별최대생활인구수"]].sum().reset_index()

# 평균 생활인구 예측
X_avg = yearly_pop[["연도"]]
y_avg = yearly_pop["시간별평균생활인구수"]
model_avg = LinearRegression().fit(X_avg, y_avg)
pred_avg_2025 = model_avg.predict([[2025]])[0]

# 그래프
plt.figure(figsize=(8, 4))
plt.plot(X_avg, y_avg, marker="o", color="blue", label="평균 생활인구")
plt.plot([2020, 2025], model_avg.predict([[2020], [2025]]), linestyle="--", color="gray", label="회귀선")
plt.title("연도별 평균 생활인구 변화 및 2025 예측")
plt.xlabel("연도")
plt.ylabel("평균 생활인구수 (합계)")
plt.xticks([2020, 2021, 2022, 2023, 2024, 2025])
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

# 최대 생활인구 예측
X_max = yearly_pop[["연도"]]
y_max = yearly_pop["시간별최대생활인구수"]
model_max = LinearRegression().fit(X_max, y_max)
pred_max_2025 = model_max.predict([[2025]])[0]

pred_avg_2025 = int(pred_avg_2025)
pred_max_2025 = int(pred_max_2025)

yearly_pop_2025 = pd.DataFrame({
    "연도": [2025],
    "시간별평균생활인구수": [pred_avg_2025],
    "시간별최대생활인구수": [pred_max_2025],
    "평균 증가율(%)": [None],  # 증가율은 계산하지 않음
    "최대 증가율(%)": [None]
})
yearly_pop = pd.concat([yearly_pop, yearly_pop_2025], ignore_index=True)

# 그래프
plt.figure(figsize=(8, 4))
plt.plot(X_max, y_max, marker="o", color="red", label="최대 생활인구")
plt.plot([2020, 2025], model_max.predict([[2020], [2025]]), linestyle="--", color="gray", label="회귀선")
plt.title("연도별 최대 생활인구 변화 및 2025 예측")
plt.xlabel("연도")
plt.ylabel("최대 생활인구수 (합계)")
plt.xticks([2020, 2021, 2022, 2023, 2024, 2025])
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

 

 

4. 연도별 쓰레기 배출량 변화 및 2025년 예측

• 마포구의 연도별 쓰레기 배출량 데이터를 바탕으로 2012년부터 2021년까지의 실제 배출량을 분석하고
  선형 회귀를 통해 2022~2025년의 배출량을 예측
• 예측값과 실제값을 결합하여 전체 추세를 시각화

# CSV 불러오기
trash_df = pd.read_csv("mapo_trash_collection_by_dong_2012_2021.csv", encoding="cp949")
trash_df.rename(columns={"구분": "연도"}, inplace=True)

# 실제 데이터 (2012~2021)
year_total = trash_df[["연도", "합계"]].copy()

# 선형 회귀 모델 학습
X_train = year_total[["연도"]]
y_train = year_total["합계"]
model = LinearRegression()
model.fit(X_train, y_train)

# 2022~2025 예측
future_years = pd.DataFrame({"연도": [2022, 2023, 2024, 2025]})
future_pred = model.predict(future_years)
future_df = pd.DataFrame({
    "연도": future_years["연도"],
    "합계": future_pred
})

# 실제 + 예측 데이터 결합
extended_total = pd.concat([year_total, future_df], ignore_index=True)

# 회귀선 계산
X_line = extended_total[["연도"]]
y_line = model.predict(X_line)

# 시각화
plt.figure(figsize=(9, 5))
plt.plot(year_total["연도"], year_total["합계"], marker="o", color="brown", label="실제 배출량")
plt.plot(extended_total["연도"], y_line, linestyle="--", color="gray", label="회귀 추세선")
plt.title("마포구 연도별 쓰레기 배출량 및 추세선 (2025년까지)")
plt.xlabel("연도")
plt.ylabel("배출량 (톤)")
plt.xticks(extended_total["연도"])
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

extended_total = extended_total.rename(columns={"합계": "쓰레기_배출량_연간_합계"})

 

5. 2020년 이후 데이터를 기반으로 한 쓰레기통 수 예측

• 마포구의 연도별 데이터 중 총 가중 매출, 생활인구(평균/최대), 연간 쓰레기 배출량은 값의 범위가 서로 상이하여
  회귀 분석 전 표준화(Standardization) 작업이 필요
• StandardScaler를 활용해 각 변수에 대해 평균 0, 표준편차 1 기준으로 정규화 수행
• 정규화된 데이터를 바탕으로 추후 쓰레기통 수와의 관계 분석 및 시각화에 활용

from sklearn.preprocessing import StandardScaler

merged_df = extended_sales.merge(yearly_pop, on="연도").merge(extended_total, on="연도")
bin_df_clean = bin_df_clean[bin_df_clean["연도"] >= 2020]
final_df = merged_df.merge(bin_df_clean, on="연도")

X = final_df[["총_가중_매출", "시간별평균생활인구수", "시간별최대생활인구수", "쓰레기_배출량_연간_합계"]]
y = final_df["쓰레기통수"]

# 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

X_scaled_df = pd.DataFrame(X_scaled, columns=X.columns)
print("\n 정규화된 각 컬럼별 값:")
print(X_scaled_df)

 정규화된 각 컬럼별 값:
    총_가중_매출  시간별평균생활인구수  시간별최대생활인구수  쓰레기_배출량_연간_합계
0 -1.620706    1.539995   -0.979481      -1.320773
1 -0.709505   -1.122828   -1.376803      -0.755227
2  0.584347    0.141409    0.358796      -0.098126
3  0.920000    0.492616    0.895501       0.692000
4  0.825864   -1.051192    1.101986       1.482126

 

# 정규화 대상 변수
features = ["총_가중_매출", "시간별평균생활인구수", "시간별최대생활인구수", "쓰레기_배출량_연간_합계", "쓰레기통수"]

# 정규화
scaler_all = StandardScaler()
scaled_all = scaler_all.fit_transform(final_df[features])

# 정규화된 데이터프레임 생성
scaled_df = pd.DataFrame(scaled_all, columns=features)
scaled_df["연도"] = final_df["연도"].values

# 시각화
fig, axes = plt.subplots(2, 2, figsize=(14, 12))
axes = axes.flatten()

for i, feature in enumerate(features[:-1]):  # 마지막은 쓰레기통수이므로 제외
    ax = axes[i]
    ax.plot(scaled_df["연도"], scaled_df[feature], marker='o', color='blue', label=f"{feature} (정규화)")
    ax.plot(scaled_df["연도"], scaled_df["쓰레기통수"], marker='s', linestyle='--', color='green', label="쓰레기통수 (정규화)")

    ax.set_title(f"{feature} vs 쓰레기통수 (정규화된 값 기준)")
    ax.set_xlabel("연도")
    ax.set_ylabel("정규화된 값")
    ax.set_xticks(scaled_df["연도"])
    ax.grid(True)
    ax.legend()

 

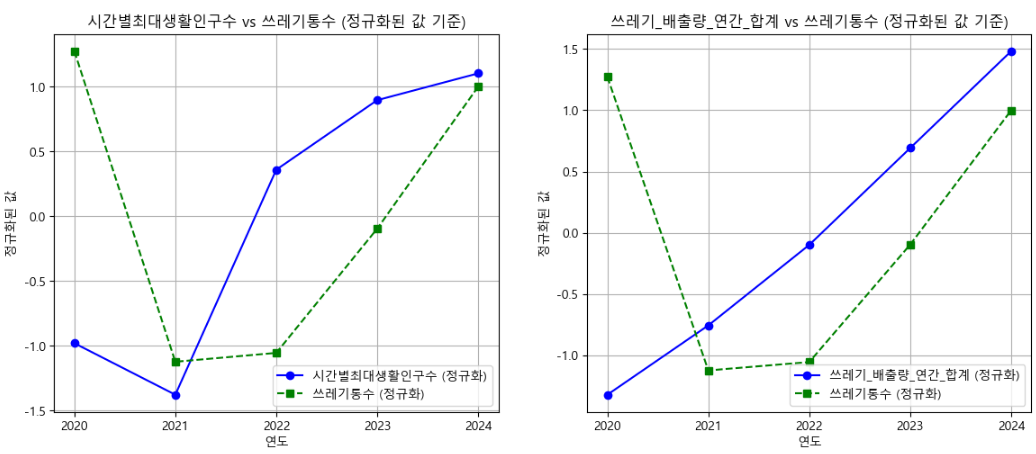
• 마포구의 가로 쓰레기통 수는 행정 정책과 민원에 따라 증가하거나 감소해왔으며, 외부 요인에 의한 변동성이 큼.
• 따라서 (2020~2024) 데이터를 기반으로 선형 회귀 모델을 학습하여, 최근 경향성을 반영한 2025년 예측값을 산출함.
• 분석에 사용된 주요 변수는 총_가중_매출, 시간별평균생활인구수, 시간별최대생활인구수, 연간 쓰레기 배출량이며, 정규화를 통해 입력값 스케일 차이를 보정함.

train_df = final_df[final_df["연도"] > 2020]

# 학습용 X, y 구성 및 정규화
X_train = train_df[["총_가중_매출", "시간별평균생활인구수", "시간별최대생활인구수", "쓰레기_배출량_연간_합계"]]
y_train = train_df["쓰레기통수"]
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)

# 회귀 모델 학습
model = LinearRegression()
model.fit(X_train_scaled, y_train)


# 2025년 예측
X_2025 = merged_df[merged_df["연도"] == 2025][["총_가중_매출", "시간별평균생활인구수", "시간별최대생활인구수", "쓰레기_배출량_연간_합계"]]
X_2025_scaled = scaler.transform(X_2025)
predicted_bin_2025 = model.predict(X_2025_scaled)[0]

print(f"\n2025년 예측 쓰레기통 수 (정규화 기준): {int(predicted_bin_2025)}개\n")
print("회귀 계수 (정규화된 입력 기준, 상대적 영향력):")
for feature, coef in zip(X.columns, model.coef_):
    print(f"{feature}: {coef:.4f}")


# 실제 값
actual_years = final_df["연도"].tolist()
actual_bins = y.tolist()

# 예측값 추가
years_with_prediction = actual_years + [2025]
X_all_scaled = scaler.transform(merged_df[merged_df["연도"].isin(years_with_prediction)][X.columns])
predicted_all_bins = model.predict(X_all_scaled)

# Plot
plt.figure(figsize=(10, 5))
plt.plot(actual_years, actual_bins, marker='o', color='green', label='실제 쓰레기통 수', linewidth=2)
plt.plot(2025, int(predicted_bin_2025), marker='X', color='red', markersize=10, label='2025 예측값')
plt.plot(years_with_prediction, predicted_all_bins, linestyle='--', color='gray', label='회귀 예측 추세선')

plt.title("마포구 연도별 가로 쓰레기통 수 및 2025년 예측")
plt.xlabel("연도")
plt.ylabel("쓰레기통 수")
plt.xticks(years_with_prediction)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

2025년 예측 쓰레기통 수 (정규화 기준): 276개

회귀 계수 (정규화된 입력 기준, 상대적 영향력):
총_가중_매출: -5.3099
시간별평균생활인구수: 0.9114
시간별최대생활인구수: -2.7676
쓰레기_배출량_연간_합계: 18.9091

 

 

가로 쓰레기통 공간 최적 배치 (격자 기반 배치 전략)

• 앞에서 계산한 종합 가중치 total_weight를 사용하여 격자 기반 최적의 배치 선정정
• 쓰레기통 총 목표 배치 수는 276개로 설정하고, 중복 배치 방지 및 밀집도 조절을 위해 최소 거리 150m 기준 적용
• 가중치(total_weight)가 높은 격자를 우선으로 선별하며, 너무 가까운 위치는 제외하고 쓰레기통을 효율적으로 배치
• 가중치 기준으로 쓰레기통 수 결정:
  • total_weight ≥ 가중치 최고값 - 0.2인 경우 → 2개 배치
  • 그 외는 1개 배치

TRASH_BIN_TOTAL = 276
MIN_DIST_METER = 150  # 최소 거리 제한 (m)
selected_centers = []
selected_info = []  # (index, count)

# 거리 계산용 좌표계로 변환
grid_gdf_utm = grid_gdf.to_crs(epsg=5181)
grid_gdf_utm['center'] = grid_gdf_utm.geometry.centroid  # 중심점 재계산

# total_weight 기준 정렬
sorted_gdf = grid_gdf_utm.sort_values(by="total_weight", ascending=False)
max_weight = sorted_gdf["total_weight"].max()
threshold = max_weight - 0.2  # 기준값 설정

current_total = 0

for idx, row in sorted_gdf.iterrows():
    pt = row['center']
    weight = row['total_weight']
    
    # 너무 가까운 기존 격자와의 거리 확인
    too_close = any(pt.distance(sel_pt) < MIN_DIST_METER for sel_pt in selected_centers)
    if too_close:
        continue

    # 가중치가 기준 이상이면 2개, 아니면 1개 배치
    bin_count = 2 if weight >= threshold else 1

    # 총 개수 초과 시 종료
    if current_total + bin_count > TRASH_BIN_TOTAL:
        break

    selected_centers.append(pt)
    selected_info.append((idx, bin_count))
    current_total += bin_count

# 결과 저장
grid_gdf['trash_bin_mark'] = 0
for idx, count in selected_info:
    grid_gdf.at[idx, 'trash_bin_mark'] = count

print(f"총 배치된 쓰레기통 수: {current_total}")
print(f"배치된 격자 수: {len(selected_info)}")

총 배치된 쓰레기통 수: 276
배치된 격자 수: 264

 

최적화된 쓰레기통 신규 배치 위치 시각화

• 생활인구, 무단투기, 상권, 공원 등의 종합 가중치(total_weight) 를 기반으로 쓰레기통을 총 276개 새롭게 배치하는 시뮬레이션
• 기존 데이터를 무시하고 처음부터 최적으로 배치한다는 가정 하에, 격자 내 가중치가 높고 서로 일정 거리(150m 이상)를 유지하도록 최적화
• 점수 기반으로 2개의 쓰레기통이 필요한 격자에는 약간의 위치 오프셋을 주어 겹치지 않도록 시각화

# 지도 생성
m = folium.Map(location=[37.55, 126.94], zoom_start=13)

# Point 객체가 있는 center 컬럼 제거 후 시각화
folium.GeoJson(
    grid_gdf.drop(columns=['center'], errors='ignore'),
    style_function=lambda feature: {
        'fillColor': 'white',
        'color': 'gray',
        'weight': 0.5,
        'fillOpacity': 0.1
    }
).add_to(m)

# 쓰레기통 마커 시각화
for _, row in grid_gdf.iterrows():
    lat, lon = row['lat'], row['lon']
    
    if row['trash_bin_mark'] == 1:
        folium.CircleMarker(
            location=[lat, lon],
            radius=6,
            color='blue',
            fill=True,
            fill_color='deepskyblue',
            fill_opacity=0.8,
            tooltip="쓰레기통 1개"
        ).add_to(m)

    elif row['trash_bin_mark'] == 2:
        offset = 0.00015  # 약 15m 거리
        folium.CircleMarker(
            location=[lat + offset, lon + offset],
            radius=6,
            color='darkblue',
            fill=True,
            fill_color='dodgerblue',
            fill_opacity=0.85,
            tooltip="쓰레기통 2개 중 첫 번째"
        ).add_to(m)

        folium.CircleMarker(
            location=[lat - offset, lon - offset],
            radius=6,
            color='darkblue',
            fill=True,
            fill_color='dodgerblue',
            fill_opacity=0.85,
            tooltip="쓰레기통 2개 중 두 번째"
        ).add_to(m)

m  # 지도 출력

기존 쓰레기통의 단계적 재배치 전략

• 기존 마포구 내 설치된 전체 쓰레기통을 한 번에 교체하거나 재배치하지 않고, 가중치가 낮은 위치의 쓰레기통부터 점차적으로 최적의 위치로 재배치
• 생활인구, 상권, 공원, 무단투기 등으로 산출된 total_weight가 낮은 위치는 활용도가 낮다고 판단하고 우선 교체 대상으로 지정.
• 기존 쓰레기통의 위치를 격자에 매핑하고, 해당 격자의 종합 가중치(total_weight) 를 점수화.
• 주변에 쓰레기통이 몰려 있는 경우, 중복성으로 인한 점수 조정(감점) 적용.
• 조정된 점수(adjusted_score)가 특정 기준 이하(예: 0.1 이하) 인 쓰레기통을 선별하여 더 유용한 위치로 이동.

 

쓰레기통 위치별 가중치 계산

• 모든 쓰레기통 위치에 대해, 어느 격자(grid_gdf)에 속하는지를 검사합니다.
• 해당 격자의 total_weight 값을 weight_score로 할당합니다.

# GeoDataFrame 변환
df_bins = pd.read_csv("mapo_street_bins_with_coords.csv")
df_bins = df_bins.dropna(subset=["위도", "경도"])

# 중복 제거
df_bins = df_bins.drop_duplicates(subset=["세부위치", "형태", "수거쓰레기종류"])

gdf_bins = gpd.GeoDataFrame(
    df_bins,
    geometry=gpd.points_from_xy(df_bins["경도"], df_bins["위도"]),
    crs="EPSG:4326"
)

# 그리드 가중치 계산
bin_scores = []
for _, bin_row in gdf_bins.iterrows():
    point = bin_row.geometry
    score = 0.0
    for _, grid_row in grid_gdf.iterrows():
        if grid_row["geometry"].contains(point):
            score = grid_row.get("total_weight", 0.0)
            break
    bin_scores.append(score)

gdf_bins["weight_score"] = bin_scores

# 좌표계 변환
gdf_bins = gdf_bins.to_crs(epsg=5181)
ADJUST_RADIUS = 50
adjusted_scores = []

for i, bin_row in gdf_bins.iterrows():
    pt = bin_row.geometry
    nearby = gdf_bins[gdf_bins.geometry.distance(pt) < ADJUST_RADIUS]
    neighbor_count = len(nearby) - 1  # 자기 제외

    base_score = bin_row["weight_score"]
    adjusted_score = base_score - (neighbor_count * 0.02) # 쓰레기통이 가까이 있으면 감점
    adjusted_score = max(adjusted_score, 0.0)
    adjusted_scores.append(adjusted_score)

gdf_bins["adjusted_score"] = adjusted_scores
gdf_bins["rank"] = gdf_bins["adjusted_score"].rank(method="min", ascending=False).astype(int)

print(gdf_bins.sort_values(by="rank").head(5)[["세부위치", "adjusted_score", "rank"]])

                  세부위치  adjusted_score  rank
199    월드컵로 30 세븐일레븐 앞        0.649365     1
95   합정역 2번 출구 KT대리점 앞        0.617364     2
281   합정역 8번 출구 횡단보도 앞        0.617364     2
246  합정역 8번 출구, 횡당보도 앞        0.617364     2
75    어울마당로 131 보승회관 앞        0.560387     5

• 0.05 이하: 🔴 빨강 (문제 있음)
• 0.05 ~ 0.1 이하: 🟡 노랑 (주의 필요)
• 0.1 초과: 🟢 초록 (정상)

 

import folium
import numpy as np

gdf_bins["adjusted_score"] = pd.to_numeric(gdf_bins["adjusted_score"], errors="coerce")

m = folium.Map(location=[37.56, 126.91], zoom_start=14)

for _, row in gdf_bins.iterrows():
    score = row.get("adjusted_score", np.nan)

    # 색상 지정
    if pd.isna(score):
        color = "gray"
    elif score <= 0.05:
        color = "red"
    elif score <= 0.1:
        color = "orange"  # folium에는 "yellow" 대신 "orange"가 더 잘 보임
    else:
        color = "green"

    # 팝업 생성
    if pd.notna(score):
        popup_html = folium.Popup(
            f"<div style='width: 200px;'><b>{row['세부위치']}</b><br>점수: {score:.3f}</div>",
            max_width=200
        )
    else:
        popup_html = folium.Popup(
            f"<div style='width: 200px;'><b>{row['세부위치']}</b><br>점수 없음</div>",
            max_width=200
        )

    # 마커 생성
    folium.Marker(
        location=[row["위도"], row["경도"]],
        popup=popup_html,
        icon=folium.Icon(color=color, icon="trash", prefix="fa")
    ).add_to(m)

# 점수 기준에 따라 색상 분류
score_bins = {
    "green": gdf_bins[gdf_bins["adjusted_score"] > 0.1],
    "orange": gdf_bins[(gdf_bins["adjusted_score"] <= 0.1) & (gdf_bins["adjusted_score"] > 0.05)],
    "red": gdf_bins[gdf_bins["adjusted_score"] <= 0.05]
}

# 색상별 쓰레기통 개수 출력
for color, subset in score_bins.items():
    print(f"{color.capitalize()} 쓰레기통 수: {len(subset)}개")

m

Green 쓰레기통 수: 241개
Orange 쓰레기통 수: 6개
Red 쓰레기통 수: 8개

 

낮은 점수 쓰레기통 제거 후 최적 위치에 재배치

• 기존 쓰레기통 중 adjusted_score ≤ 0.1 (빨강/주황) 인 위치는 효율이 낮다고 판단하여 제거.
• 제거 후 남은 초록색 쓰레기통의 위치는 유지.
• 제거된 개수만큼만 새롭게 배치하되, 기존 쓰레기통(초록색)과 일정 거리(150m) 이상 떨어진 위치에만 신규 배치.
• 격자의 total_weight 기준으로 우선순위 정렬 후, 높은 위치부터 점진적으로 배치.

 

# 제거 대상(점수 낮은) 쓰레기통 제외
green_bins = gdf_bins[gdf_bins["adjusted_score"] > 0.1].copy()

# 제거 대상 수 확인
removed_count = len(gdf_bins) - len(green_bins)
print(f"제거된 쓰레기통 수: {removed_count}")

# 남은 초록 쓰레기통들의 위치 목록 (UTM 좌표계)
green_bins_utm = green_bins.to_crs(epsg=5181)
existing_locations = list(green_bins_utm.geometry)

# 새로운 쓰레기통 총 개수 계산 276개로 설정 
NEW_BIN_COUNT = TRASH_BIN_TOTAL - len(green_bins)

# grid 준비
grid_gdf_utm = grid_gdf.to_crs(epsg=5181)
grid_gdf_utm['center'] = grid_gdf_utm.geometry.centroid
grid_gdf_utm = grid_gdf_utm.sort_values(by="total_weight", ascending=False)

MIN_DIST = 150  # 150m 이상 떨어진 위치만 허용
new_selected_centers = []
new_selected_indices = []
new_bin_total = 0

for idx, row in grid_gdf_utm.iterrows():
    pt = row['center']
    weight = row['total_weight']

    # 기존 초록 쓰레기통과 너무 가까우면 배치 제외
    if any(pt.distance(existing) < MIN_DIST for existing in existing_locations):
        continue
    if any(pt.distance(new) < MIN_DIST for new in new_selected_centers):
        continue

    bin_count = 2 if weight >= (grid_gdf_utm["total_weight"].max() - 0.2) else 1

    if new_bin_total + bin_count > NEW_BIN_COUNT:
        break

    new_selected_centers.append(pt)
    new_selected_indices.append((idx, bin_count))
    new_bin_total += bin_count

# grid_gdf에 새로운 쓰레기통 배치 마킹
grid_gdf['new_bin_mark'] = 0
for idx, count in new_selected_indices:
    grid_gdf.at[idx, 'new_bin_mark'] = count

print(f"재배치된 쓰레기통 수: {new_bin_total}")

제거된 쓰레기통 수: 14
재배치된 쓰레기통 수: 35

 

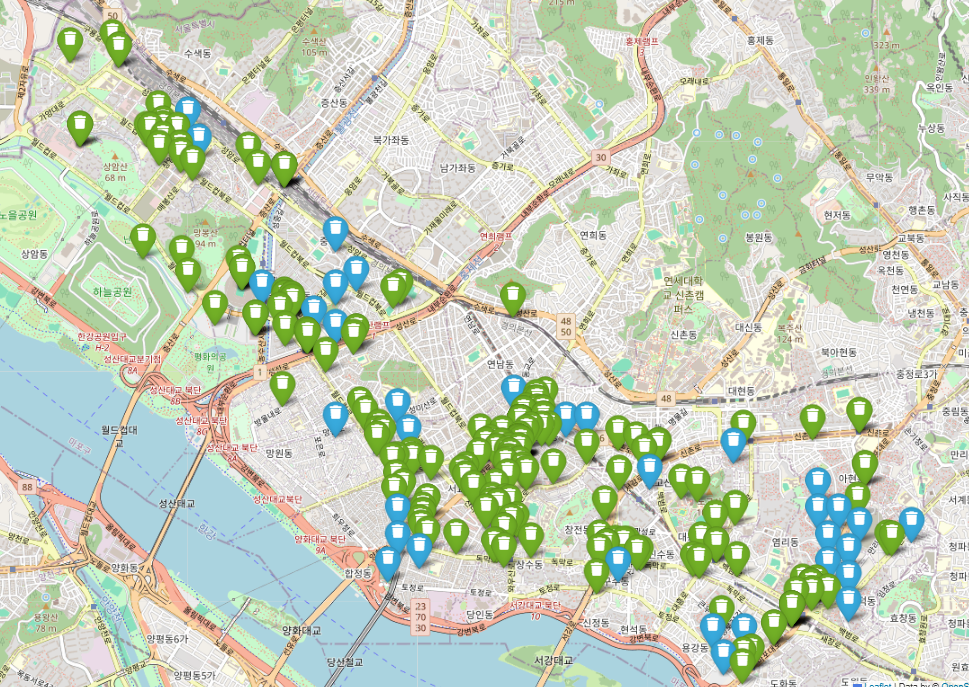
마커 색상 설명

• 초록색 마커
  현재 위치에 있는 기존 쓰레기통 중 점수가 높은 위치
  (adjusted_score > 0.1)
  → 제거하지 않고 유지한 쓰레기통
• 파란색 마커
  기존 저평가된 쓰레기통을 제거한 후,
  새롭게 재배치된 쓰레기통의 위치
  → 가중치가 높은 격자 중 기존 쓰레기통과의 최소 거리 조건을 만족하는 위치에 배치됨

import folium

# 지도 생성
m = folium.Map(location=[37.55, 126.94], zoom_start=13)

# 기존 초록 쓰레기통 (score > 0.1) → 파란색 마커
for _, row in gdf_bins[gdf_bins["adjusted_score"] > 0.1].iterrows():
    folium.Marker(
        location=[row["위도"], row["경도"]],
        popup=f"{row['세부위치']}<br>점수: {row['adjusted_score']:.2f}",
        icon=folium.Icon(color="green", icon="trash", prefix="fa")
    ).add_to(m)

# 재배치된 쓰레기통 시각화 → 기본 초록 마커
grid_gdf_plot = grid_gdf.to_crs(epsg=4326)

for _, row in grid_gdf_plot.iterrows():
    lat = row['lat']
    lon = row['lon']
    
    if row.get('new_bin_mark', 0) > 0:
        folium.Marker(
            location=[lat, lon],
            popup=f"재배치 쓰레기통",
            icon=folium.Icon(color="blue", icon="trash", prefix="fa")
        ).add_to(m)

m

 

 

결과 요약 및 분석 개요

이번 프로젝트는 마포구의 가로 쓰레기통 설치를 정량적 데이터 기반으로 최적화하기 위한 분석 작업으로, 다음과 같은 두 가지 핵심 목표를 달성하였습니다:

 

1. 공간 기반 분석을 통한 최적 설치 위치 도출
   • 다음과 같은 실제 도시 데이터를 수집 및 결합하여, 마포구를 100m x 100m 격자 단위로 나눈 후 각 격자의 상대적 수요를 정량화:
     • 생활인구 데이터: 유동 인구가 많은 지역 파악
     • 상권 매출 데이터: 쓰레기 발생 가능성이 높은 상업지역 반영
     • 공원 위치 데이터: 쓰레기통이 필요한 공공 공간 고려
     • 무단투기 발생 위치: 민감 지역 가중치 보정
2. 연도별 추세 분석을 통한 적정 설치 수 예측
   • 마포구 공공 데이터를 바탕으로, 생활인구, 상권 매출, 연간 쓰레기 배출량의 변화를 분석하여 쓰레기통 수요를 추정
   • 표준화 및 회귀분석을 통해 도출된 결과를 기반으로, 2025년에 필요한 쓰레기통의 수를 의미있는 값으로 예측함

• 최종적으로 각 요소를 표준화하고 가중합하여 total_weight를 계산
• 가중치가 높은 격자부터 우선 배치하되, 최소 거리(150m) 기준 필터링을 적용하여 중복 설치 방지
• 최종적으로, 총 쓰레기통 수(예: 276개) 내에서 효율적인 위치를 선정함

 

기대 효과

• 과학적 기반의 정책 설계
  감에 의존한 기존의 민원 기반 설치 방식에서 벗어나, 정량적 데이터를 바탕으로 쓰레기통의 적정 수와 위치를 추정함으로써 과학적 행정 구현 가능
• 청결도 및 시민 만족도 향상
  유동 인구 및 쓰레기 배출량이 높은 곳에 쓰레기통이 설치되어, 무단투기 감소, 거리 청결 유지, 시민 만족도 향상에 기여할 수 있음
• 예산 및 공간 자원의 효율적 사용
  불필요한 중복 설치 없이, 필요한 곳에만 설치함으로써 자원 낭비를 최소화하고, 한정된 예산을 최적화할 수 있음
• 확장 가능한 정책 도구
  이번 분석은 마포구를 대상으로 하였으나 다른 자치구나 시설물 배치 문제(예: 벤치, CCTV) 등으로도 확장 가능하며, 지속적으로 데이터가 축적되면 더 정화한 예측도 가능